A Journey Through Fastbook (AJTFB) - Chapter 9: Tabular Modeling
In chapter of 8 of "Deep Learning for Coders with fastai & PyTorch" numbers*. "Structured" or "tabular" data describes datasets that look like an Excel spreadsheet or a relational database table, of which, it may be a composed of both categorical and/or real numbers. Working with such data is the subject of chapter 9, so lets go!
- Tabular Modeling
- Categorical Embeddings
- Imports
- Data preparation
- Creating our TabularPandas
- Approach 1: Decision Trees
- Approach 2: Random Forests
- Step 1: Define your Random Forest
- Step 2: Determine why our validation set is worse than training
- Model Interpretation
- How confident are we in our predictions using a particular row of data?
- Which columns are the strongest predictors (and which can we ignore)?
- Which columns are effectively redundant?
- How do find the relationship between two predictors (columns)?
- For predicting a specific row of data, what were the most important factors and how did they influence the prediction?
- The "Extrapolation" problem
- Approach 3: Neural Networks
- Approach 4: Boosting
- Other things to try
- In summary
- Resources
Other posts in this series:
A Journey Through Fastbook (AJTFB) - Chapter 1
A Journey Through Fastbook (AJTFB) - Chapter 2
A Journey Through Fastbook (AJTFB) - Chapter 3
A Journey Through Fastbook (AJTFB) - Chapter 4
A Journey Through Fastbook (AJTFB) - Chapter 5
A Journey Through Fastbook (AJTFB) - Chapter 6a
A Journey Through Fastbook (AJTFB) - Chapter 6b
A Journey Through Fastbook (AJTFB) - Chapter 7
A Journey Through Fastbook (AJTFB) - Chapter 8
Tabular Modeling
What is it?
"Tabular modeling takes data in the form of a table (like a spreadsheet or CSV). The objective is to predict the value of one column based on the values in the other columns." Tabular data is also called "structured data" while "unstructured data" represents things like text, images, audio, etc...
Why is it important?
Though it is reported that 80-90% of data is unstructured (think images, text, audio), ironically, it appears that the vast majority of "real world" machine learning is concerened with tabular/structured data.
If you are just starting out with Data Science you should know that still the vast majority of DS problems in the industry concern structured/tabular data. This is what you should focus on in order to make a professional inroad.
— Bojan Tunguz (@tunguz) February 23, 2022
1/3
What are they?
-
For structured data, ensembles of decision trees (e.g., random forests and gradient boosting machines like XGBoost).
-
For unstructured data, multilayered neural networks learned with SGD.
Note: "... ensembles of decision trees tend to train faster, are often easier to interpret, do not require special GPU hardware for inference at scale, and often require less hyperparameter tuning.Important: Since a "critical step of interpreting a model of tabular data is significantly easier for decesion tree ensembles ... ensembles of decision trees are our first approach for analyzing a new tabular dataset"Important: Neural networks will considered when "there are some high-cardinality categorical variables" or there are columns with unstructured data. A example of a high "cardinality" (e.g., the number of discrete levels representing the categories) would be something like zip code.
See pages 282-284 for more discussion on the pros/cons of decision trees and neural networks for tabular data.
Categorical Embeddings
Continuous v. Categorical
Continuous variables "contain a real numbers that be fed into a model directly and are meaningful in and out of themselves. Examples include "age" and "price".
Categorical variables "contain a number of discrete levels, such as 'movie ID,' for which addition and multiplication don't have any meaning (even if they're stored as numbers). Other examples include dates, columns indicating "sex", "gender", "department", etc...
How do we represent "categorical" data?
We learned this in chapter 8, we represent such data via entity embeddings.
Because "an embedding layer is exactly equivalent to placing an ordinary linear layer after every one-hot-encoded input layer ... the embedding transforms the categorical variables into inputs that are both continuous and meaningful."
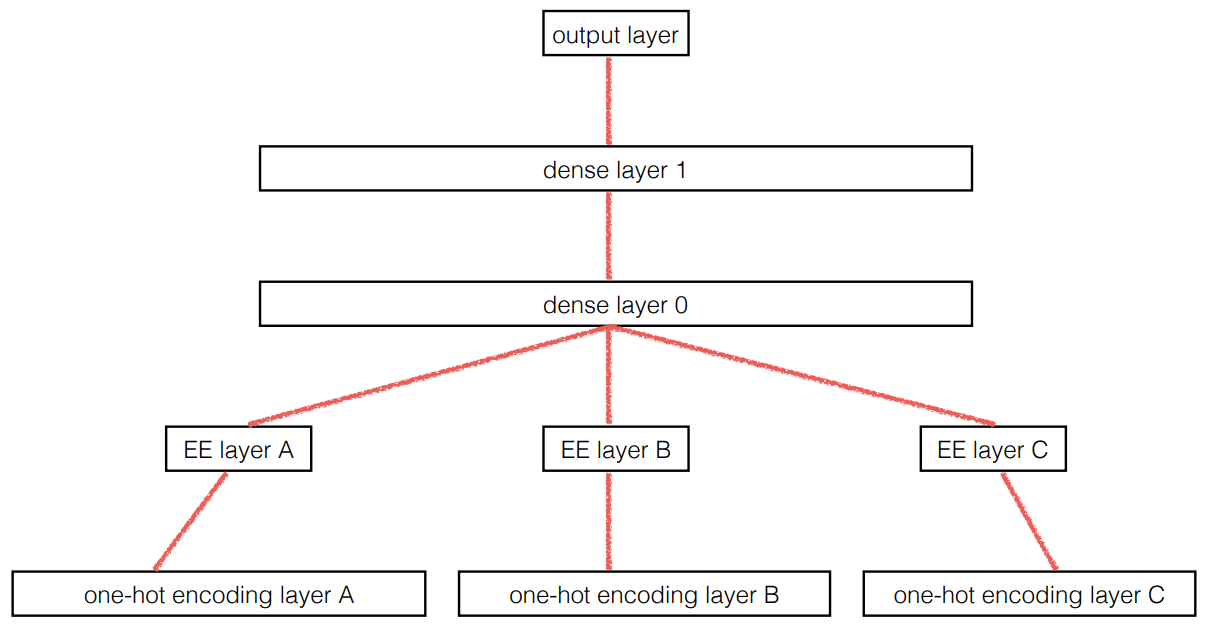
In other words ...
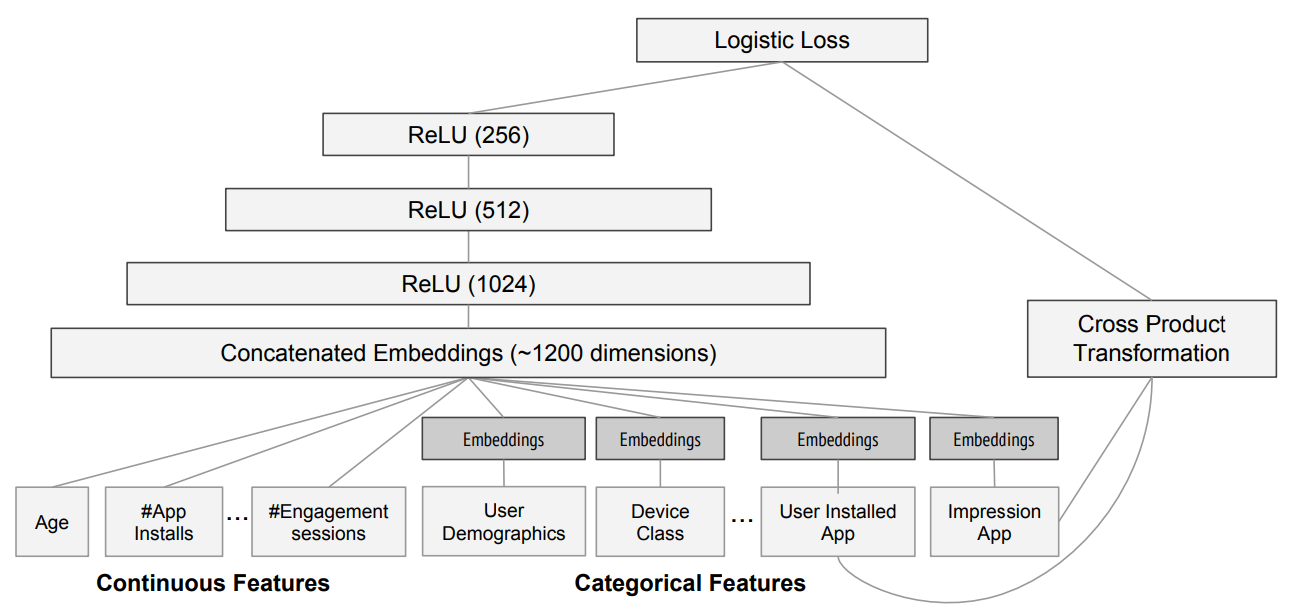
from kaggle import api
from dtreeviz.trees import *
from fastai.tabular.all import *
from IPython.display import Image, display_svg, SVG
from pandas.api.types import is_string_dtype, is_numeric_dtype, is_categorical_dtype
from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeRegressor,export_graphviz
pd.options.display.max_rows = 20
pd.options.display.max_columns = 8
Step 1: Get the data
We'll be getting the data from kaggle. If you're running on colab, check out these instructions for getting setup with the kaggle API
path = Path("bluebook")
path
if not path.exists():
path.mkdir()
api.competition_download_cli("bluebook-for-bulldozers", path=path)
file_extract(path/"bluebook-for-bulldozers.zip")
path.ls(file_type="text")
Step 2: EDA
low_memory=False unless Pandas acutally runs out of memory." The default = True (will look only at the first few rows of data to infer column datatypes).
train_df = pd.read_csv(path/"TrainAndValid.csv", low_memory=False)
test_df = pd.read_csv(path/"Test.csv", low_memory=False)
train_df.columns
describe() is a method that gives you some basic stats for each column.
train_df.describe().T
advanced_describe() is a method I created that builds on top of the default describe() method to include stats on missing and unique values (which are both very helpful in terms of cleanup, understanding potential issues, and in determining the size of your embeddings for categorical data). For categorical variables with few discrete levels, this method will also show you what they are.
advanced_describe(train_df)
train_df.ProductSize.unique()
sizes = ['Large', 'Large / Medium', 'Medium', 'Small', 'Mini', 'Compact']
train_df.ProductSize = train_df.ProductSize.astype("category")
train_df.ProductSize = train_df.ProductSize.cat.set_categories(sizes, ordered=True) # note: "inplace=True" is depreciated as of 1.30
train_df.ProductSize.unique()
Handling Your Dependent Variable(s)
"You should think carefully about which metric, or set of metrics, actually measures the notion of model quality that matters to you ... in this case, Kaggle tells us [our measure is] root mean squared log error (RMLSE)" and because of this we need to make our target the log of the price "so that the m_rmse of that value will give us what we ultimately need."
dep_var = "SalePrice"
train_df[dep_var] = np.log(train_df[dep_var])
Handling Dates
Dates are "different from most ordinal values in that some dates are qualitatively different from others in a way that is often relevant to the systems we are modeling." As such, we want the model to know if whether the day is a holiday, or part of the weekend, or in a certain month, etc... is important. To do this, "we **replace every date column with a set of date metadata columns, such as holiday, day of week, and month" = categorical data that might be very useful!
Can use fastai's add_datepart() function to do this.
train_df = add_datepart(train_df, "saledate")
test_df = add_datepart(test_df, "saledate")
[col for col in train_df.columns if col.startswith("sale")]
For this we can use fastai's TabularPandas class (allows us to apply TabularProc transforms to the DataFrame it wraps to do things like fill missing values, make columns categorical, etc...).
Categorify: "a TabularProc that replaces a column with a numeric categorical column"
FillMissing: "a TabularProc that replaces missing values with the median of the column, and **creates a new Boolean column that is set to True for any row where the value was missing. You can change this fill strategy via thefill_strategy` argument.
procs = [Categorify, FillMissing]
cont, cat = cont_cat_split(train_df, 1, dep_var=dep_var)
Step 2: Define our training and validation splits
What is the difference between validation and test sets again?
Recall that a validation set "is data we hold back from training in order to ensure that the training process does not overfit on the training data" ... while a test set "is data that is held back from ourselves in order to ensure that we don't overfit on the validation data as we export various model architectures and hyperparameters."
Because this is a time series problem, we'll make the validation set include data for the last 6 months of the full training set, and the training set everything before that. See p.291 for more on this!
cond = (train_df.saleYear < 2011) | (train_df.saleMonth < 10)
train_idxs = np.where(cond)[0]
valid_idxs = np.where(~cond)[0]
splits = (list(train_idxs), list(valid_idxs))
to = TabularPandas(train_df, procs, cat, cont, y_names=dep_var, splits=splits)
type(to)
TabularPandas behaves a lot like a fastai Datasets object, including train and valid attributes"
len(to.train), len(to.valid)
to.show(3)
to.items.head(3)
We can see that mapping via the classes attribute:
to.classes["ProductSize"]
TabularPandas object so you don’t have to process the data again
save_pickle(path/"to.pkl", to)
# load from filesystem
to = load_pickle(path/"to.pkl")
Approach 1: Decision Trees
"A decision tree asks a series of binary (yes or no) questions about the data. After each question, the data at that part of the tree is split between a Yes and a No branch.... After one or more questions, either a prediction can be made on the basis of all previous answers or another question is required."
"... for regression, we take the target mean of the items in the group"
train_xs, train_y = to.train.xs, to.train.y
valid_xs, valid_y = to.valid.xs, to.valid.y
m = DecisionTreeRegressor(max_leaf_nodes=4)
m.fit(train_xs, train_y)
draw_tree(m, train_xs, size=7, leaves_parallel=True, precision=2)
What is in each box above?:
- The decision criterion for the best split that was found
- "samples": The # of examples in the group
- "value": The average value of the target for that group
- "squared_error": The MSE for that group
Note: "The top node represents the initial model before any splits have been done, when all the data is in one group. This is the simplest possible model. It is the result of asking zero questions and will always predict the value to be the average value of the whole dataset."
A "leaf node" is a node "with no answers coming out of them, because there are no more questions to be answered."
See p.293 for more on intrepreting the diagram above.
samp_idx = np.random.permutation(len(train_y))[:500]
dtreeviz(
m,
train_xs.iloc[samp_idx],
train_y.iloc[samp_idx],
train_xs.columns,
dep_var,
fontname="DejaVu Sans",
scale=1.6,
label_fontsize=10,
orientation="LR"
)
"This shows a cart of the distribution of the data for each split point"
dtreeviz to find problems with the data.
For example, you can see there is a problem with "YearMade" as a bunch of tractors show they are made in the year 1000. The likely explanation is that if they don't have the info on a tractor, they set it = 1000 to indicate "Unknown".
We can replace this with something like 1950 to make the visuals more clear ...
train_xs.loc[train_xs["YearMade"] < 1900, "YearMade"] = 1950
valid_xs.loc[valid_xs["YearMade"] < 1900, "YearMade"] = 1950
samp_idx = np.random.permutation(len(train_y))[:500]
dtreeviz(
m,
train_xs.iloc[samp_idx],
train_y.iloc[samp_idx],
train_xs.columns,
dep_var,
fontname="DejaVu Sans",
scale=1.6,
label_fontsize=10,
orientation="LR"
)
m = DecisionTreeRegressor()
m.fit(train_xs, train_y)
def r_mse(preds, targs):
return round(math.sqrt(((preds - targs)**2).mean()), 6)
def m_rmse(m, xs, y):
return r_mse(m.predict(xs), y)
m_rmse(m, train_xs, train_y)
m_rmse(m, valid_xs, valid_y)
What does the above indicate?
That we might be overfitting ... badly (because our training set is perfect and our validation set not so much).
Why are we overfitting?
Because "we have nearly as many leaf nodes as data points ... sklearn's default settings allow it to continue splitting nodes until there is only one item in each leaf node." See pp.295-296 for more intuition on why trees overfit.
m.get_n_leaves(), len(train_xs)
m = DecisionTreeRegressor(min_samples_leaf=25)
m.fit(to.train.xs, to.train.y)
m_rmse(m, to.train.xs, to.train.y), m_rmse(m, to.valid.xs, to.valid.y)
min_samples_leaf=25 = "Stop when all leaf nodes have a minimum of 25 samples"
A note on categorical variables
Decision trees **don't have embedding layers - "so how can these untreated categorical variables do anything useful"?
Answer: "It just works!"
get_dummies, "there is not really any evidence that such an approach improves the end result."
See p.297 for more about why OHE aren't necessary and why decision tree just work with categorical variables out-of-the-box.
Approach 2: Random Forests
A random forest "is a model that averages the predictions of a large number of decision trees, which are generated by randomly varying various parameters that specify what data is used to train the tree (what columns and rows are included in each tree) and other tree parameters"
Why does it work so well?
Because it utlizes bagging.
What is "bagging"?
From the "Bagging Predictors" paper ... "Bagging predictors is a method for generating multiple versions of a predictor and using these to get an aggregated predictor.... The multiple versions are formed by making bootstrap replicates (a randomly chosen subset of rows) of the learning set."
This means that we can improve the performance of a model by training it multiple times with a different random subset of the data each time, and then averaging the predictions.
See p.298 for more details on how bagging works.
def fit_rf(xs, y, n_estimators=40, max_samples=200_000, max_features=0.5, min_samples_leaf=5, **kwargs):
return RandomForestRegressor(
n_jobs=-1, # Tells sklearn to use all our CPUs to build the trees in parallel
n_estimators=n_estimators, # The number of trees
max_samples=max_samples, # The number of rows to sample for training ea. tree
max_features=max_features, # The number of columns to sample at each split
min_samples_leaf=min_samples_leaf, # Stop when all leaf nodes have at least this number of samples
oob_score=True
).fit(xs, y)
m = fit_rf(train_xs, train_y)
m_rmse(m, train_xs, train_y), m_rmse(m, valid_xs, valid_y)
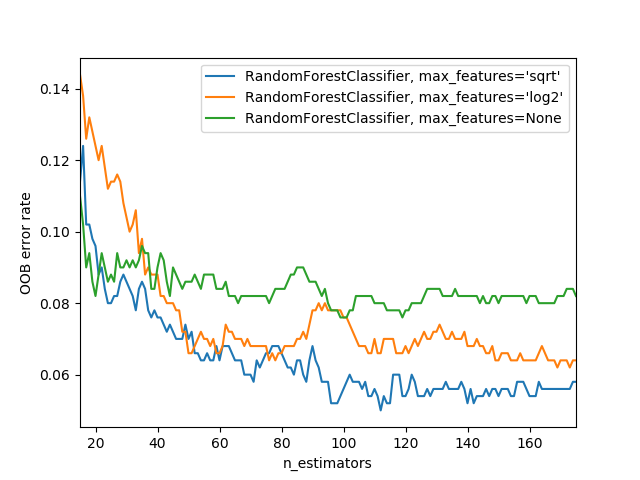
Recommended hyperparameter values:
-
n_estimators: "as high a number as you have time to train ... more trees = more accurate -
max_samples: default (200,000) -
max_features: default ("auto") or 0.5 -
min_samples_leaf: default (1) or 4Tip: Bigger forests using a smalle subset of features tens to be better (see chart below)
How to get the predictions for a SINGLE tree?
tree_preds = np.stack([t.predict(valid_xs.values) for t in m.estimators_]) # added .values (see: https://stackoverflow.com/a/69378867)
r_mse(tree_preds.mean(0), valid_y)
How does n_estimators impact model performance?
To answer this, we can increment the number of trees we use in our predictions one at a time like so:
plt.plot([r_mse(tree_preds[:i+1].mean(0), valid_y) for i in range(40)])
Step 2: Determine why our validation set is worse than training
"The OOB error is a way of measuring prediction error in the training dataset" based on rows not used in the training of a particular tree. "This allows us to see whether the model is overfitting, without needing a separate validation set."
"... out-of-bag error is a little like imagining that every tree therefore also has its own validation set" based on the prediction of rows not used in its training.
r_mse(m.oob_prediction_, train_y)
How confident are we in our predictions using a particular row of data?
Answer: "use the standard deviation of predictions across the trees, instead of just the mean. This tells us the relative confidence of predictions"
preds = np.stack([t.predict(valid_xs.values) for t in m.estimators_])
preds.shape #=> (# of trees, # of predictions)
preds_std = preds.std(0) # get rid of first dimension (the trees)
preds_std[:5]
def rf_feature_importance(m, df):
return pd.DataFrame({"cols": df.columns, "imp": m.feature_importances_}).sort_values("imp", ascending=False)
def plot_fi(fi_df):
return fi_df.plot("cols", "imp", "barh", figsize=(12,7), legend=False)
fi_df = rf_feature_importance(m, train_xs)
# Let's look at the 10 most important features
fi_df[:10]
plot_fi(fi_df[:30])
See p.304 for how feature importance is calculated.
cols_to_keep = fi_df[fi_df.imp > 0.005].cols
len(cols_to_keep)
train_xs_keep = train_xs[cols_to_keep]
valid_xs_keep = valid_xs[cols_to_keep]
m = fit_rf(train_xs_keep, train_y)
m_rmse(m, train_xs_keep, train_y), m_rmse(m, valid_xs_keep, valid_y)
The accuracy is about the same as before, but the model is much more interpretable ...
len(train_xs.columns), len(train_xs_keep.columns)
plot_fi(rf_feature_importance(m, train_xs_keep[:30]))
cluster_columns(train_xs_keep)
How do we determine similarity?
"The most similar paris are found by calculating the rank correlation, which means that all the values are replaced with their rank ... and then the correlation is calculated.
How do we know if a feature is "redundant" and can be dropped?
Answer: By removing potentially redundant variables one at a time
"We don't need [the model] to be very accurate" so we can use a lower max_samples and a higher min_samples_leaf. We just want to see the effect it has by removing certain columns using the OOB score ("a number returned by sklearn that ranges between 1.0 for a perfect model and 0.0 for a random model."
def get_oob(df, y):
m = RandomForestRegressor(n_estimators=10, min_samples_leaf=15, max_samples=50_000, max_features=0.5, n_jobs=-1, oob_score=True)
m.fit(df, y)
return m.oob_score_
Our baseline:
get_oob(train_xs_keep, train_y)
Try removing redundant features one at a time:
redundant_cols = [
'saleYear', 'saleElapsed', 'ProductGroupDesc', 'ProductGroup',
'fiModelDesc', 'fiBaseModel', 'Hydraulics_Flow', 'Grouser_Tracks', 'Coupler_System'
]
{c:get_oob(train_xs_keep.drop(c, axis=1), train_y) for c in redundant_cols}
Now try dropping multiple variables (one from each of the tightly aligned pairs we noticed above), and compare accuracy:
cols_to_drop = ["saleYear", "ProductGroupDesc", "fiBaseModel", "Grouser_Tracks"]
get_oob(train_xs_keep.drop(cols_to_drop, axis=1), train_y)
Assuming that its not much worse, create new DataFrames and save ...
train_xs_final = train_xs_keep.drop(cols_to_drop, axis=1)
valid_xs_final = valid_xs_keep.drop(cols_to_drop, axis=1)
# save to filesystem
save_pickle(path/"train_xs_final.pkl", train_xs_final)
save_pickle(path/"valid_xs_final.pkl", valid_xs_final)
... then load them back in later
train_xs_final = load_pickle(path/"train_xs_final.pkl")
valid_xs_final = load_pickle(path/"valid_xs_final.pkl")
m = fit_rf(train_xs_final.values, train_y)
m_rmse(m, train_xs_final.values, train_y), m_rmse(m, valid_xs_final.values, valid_y)
First, check the count of values per category:
p = valid_xs_final["ProductSize"].value_counts().sort_index().plot.barh()
c = to.classes["ProductSize"]
plt.yticks(range(len(c)), c)
x = valid_xs_final["YearMade"].hist()
Second, built a partial dependence plot
See pp.309-10 for info on how to do this, but in essence, we are attempting to isolate the effects of changes to a single variable.
from sklearn.inspection import PartialDependenceDisplay
fig, ax = plt.subplots(figsize=(12,4))
PartialDependenceDisplay.from_estimator(m, valid_xs_final, ["YearMade", "ProductSize"], grid_resolution=20, ax=ax)
Intrepretation
The "YearMade" plot makes sense as it shows a linear relationship with price ("remember that our dependent variable is after taking the logarithm, so this means that in practice there is an exponential increase in price). Again, this is expected given that depreciation = "a multiplicative factor over time ... varying year made ought to show an exponential relationship to sales price"
The "ProductSize" should raise concerns, "it shows that for the final group, which we saw is for missing values, has the lowest price.
What is "data leakage"?
"The introduction of information about the target of a data mining problem, which should not be legitimately available to mine from." The idea is that you're cheating by introducing something by way of the independent variables that biases your predictions favorably that you won't be able to utlize at inference time. See p.311-12 for examples.
How to determine if you have data leakage?
From p.321 ... "build a model and then ...
- Check whether the accuracy of the model is too good to be true.
- Look for important predictors that don't make sense in pratice.
- Look for partial dependence plot results that don't make sense in practice. (see above)
Tip: "... often a good idea to build a model first and then do you data cleaning rather than vice versa ... can help you identify potentially problematic data issues.
For predicting a specific row of data, what were the most important factors and how did they influence the prediction?
Answer: Use treeinterpreter. Note that:
prediction = the prediction made by RF
bias = the prediction based on taking the mean of the dependent variable (the root model for every tree)
contributions = "tells us the total change in prediction due to each of the independent variables.
"Therfore, the sum of contributions plus bias must equal the prediction for each row!
from treeinterpreter import treeinterpreter
row = valid_xs_final.iloc[:5]
pred, bias, contributions = treeinterpreter.predict(m, row.values)
pred[0], bias[0], contributions[0].sum()
What is the best waty to visualize this?
Answer: A waterfull plot will show us "how the positive and negative contributions from all the independent variables sum up to create the final prediction."
import waterfall_chart
waterfall_chart.plot(valid_xs_final.columns, contributions[0], threshold=0.08, rotation_value=45, formatting="{:,.3f}")
Where is this information useful?
Answer: In production "rather than during model development. You can use it to provide useful information to users of your data product about underlying reasoning behind the predictions."
The "Extrapolation" problem
See. pp.315-316.
How do determine if our "test set" is distributed in the same way as our "training set", and if it isn't, what columns are causing the difference?
Answer: Use a random forest where we "try to predict whether a row is in the validation set or training set."
combined_df = pd.concat([train_xs_final, valid_xs_final])
is_valid = np.array([0]*len(train_xs_final) + [1]*len(valid_xs_final))
ood_m = fit_rf(combined_df, is_valid)
rf_feature_importance(ood_m, combined_df)[:6]
"This shows that three columns differ significantly between the training and validation sets: saleElapsed, SalesID, and MachineID'
See p.317 for infering what this is.
What to do with this info?
Answer: Compare the effects of removing each of these columns with the original model
m = fit_rf(train_xs_final, train_y)
print("orig:", m_rmse(m, valid_xs_final, valid_y))
for c in ("SalesID", "saleElapsed", "MachineID"):
m = fit_rf(train_xs_final.drop(c, axis=1), train_y)
print(c, m_rmse(m, valid_xs_final.drop(c, axis=1), valid_y))
"... looks like we should be able to remove SaleID and MachineID without losing any accuracy"
time_vars = ["SalesID", "MachineID"]
train_xs_final_time = train_xs_final.drop(time_vars, axis=1)
valid_xs_final_time = valid_xs_final.drop(time_vars, axis=1)
m = fit_rf(train_xs_final_time, train_y)
m_rmse(m, valid_xs_final_time, valid_y)
is_valid for ALL datasets!
"It can often uncovere subtle domain shift issues that you may otherwise miss.
"Often, old data shows relationships that just aren't valid anymore"
train_xs["saleYear"].hist()
recent_sales = train_xs["saleYear"] > 2004
train_xs_recent = train_xs_final_time[recent_sales]
train_y = train_y[recent_sales]
m = fit_rf(train_xs_recent, train_y)
m_rmse(m, train_xs_recent, train_y), m_rmse(m, valid_xs_final_time, valid_y)
nn_df = pd.read_csv(path/"TrainAndValid.csv", low_memory=False)
sizes = ['Large', 'Large / Medium', 'Medium', 'Small', 'Mini', 'Compact']
nn_df.ProductSize = nn_df.ProductSize.astype("category")
nn_df.ProductSize = nn_df.ProductSize.cat.set_categories(sizes, ordered=True) # note: "inplace=True" is depreciated as of 1.30
nn_df[dep_var] = np.log(nn_df[dep_var])
nn_df = add_datepart(nn_df, "saledate")
nn_df_final = nn_df[list(train_xs_final_time.columns) + [dep_var]]
fastai uses the max_card to determine what columns should be treated as categoricals ... "Embedding sizes larger that 10,000 should generaly be used only after you've tested whether there are better ways to group the variable"
nn_cont, nn_cat = cont_cat_split(nn_df_final, max_card=9000, dep_var=dep_var)
Therfore, "saleElapsed" needs to be made into a continous variable ... which it alread is
nn_cont
How to find the cardinality of each categorical?
nn_df_final[nn_cat].nunique()
"... two variables pertaining to the 'model' of the equipment, both with similar very high cardinalities, suggests that they may contain similar, redundant information."
cols_to_drop = ["fiModelDescriptor"]
train_xs_recent2 = train_xs_recent.drop(cols_to_drop, axis=1)
valid_xs_recent2 = valid_xs_final_time.drop(cols_to_drop, axis=1)
m2 = fit_rf(train_xs_recent2, train_y)
m_rmse(m2, train_xs_recent2, train_y), m_rmse(m2, valid_xs_recent2, valid_y)
nn_cat.remove("fiModelDescriptor")
print(nn_cont)
print(nn_cat)
nn_procs = [Categorify, FillMissing, Normalize]
nn_to = TabularPandas(nn_df_final, nn_procs, nn_cat, nn_cont, splits=splits, y_names=dep_var)
dls = nn_to.dataloaders(bs=1024)
y_range for regression models
y = nn_to.train.y
y.min(), y.max()
from fastai.tabular.all import *
learn = tabular_learner(dls, y_range=(8, 12), layers=[500,250], n_out=1, loss_func=F.mse_loss)
learn.lr_find()
learn.fit_one_cycle(5, 1e-2)
preds, targs = learn.get_preds()
r_mse(preds, targs)
learn.save("nn")
Approach 4: Boosting
Here "we add models instead of averaging them" (as compared to ensembling). See p.323-24 for all the details, but here's how it works in general:
- Train small model that underfits
- Get predictions for model from #1
- Get the "residuals" ('the error for each point in the training set') by subtracting the predictions from the targets.
- Go back to step 1, "but instead of using the original targets, use the residuals as the targets for training.
- Continue stesp 1-4 until you need to stop (e.g., max number of trees, you start overfitting, etc...)
Steps 3-4 are the bread and butter of things.
Some go as far as saying that such models are all you need :)
XGBoost Is All You Need
— Bojan Tunguz (@tunguz) March 30, 2022
Deep Neural Networks and Tabular Data: A Surveyhttps://t.co/Z2KsHP3fvp pic.twitter.com/uh5NLS1fVP
How do you make predictions with an ensemble of boosted trees?
Answer: By calculating the predictions from each tree and then adding them all together.
XGBoost and sklearn's HistGradientBooting models are legit ML models to try ...
Here are my top used ML algos for tabular data problems:
— Bojan Tunguz (@tunguz) April 22, 2022
1. XGBoost
2. HistGradientBoosting
3. Logistic regression/ Ridge regression
4. LightGBM
5. MLP
6. A blend of 1. And 5.
Other things to try
Ensembling (pp.322-23)
This is a form of "bagging" where averaging the predictions of models trained using different algorithms, each of which it is reasonable to expect would produce differnt kinds of errors, would likely product better predictions.
Combining embeddings with other models (pp.324-25)
"... shows that you can get much of the performance improvement of a neural network without having to use a neural network as inference time" by using the embeddings as inputs (which are just array lookups) to small decision tree ensemble!
In summary
"This will give you a strong baseline ... can then use that model for feature selection and partial dependence analysis to get a better understanding of your data."
Pros/Cons of each approach:
Random forests: Pros:
- Easiest to train
- Resiliant to hyperparameter choices
- Require little preprocessing
- Fast to train
- Should not overfit if you have enough trees Cons:
- Can be less accurate (esp. if extrapolation is required "such as predicting future time periods."
Gradient boosting machines (GBMs): Pros:
- Often more accurate than random forests Cons:
- Sensitive to hyperparmeter choices
- Can overfit
Neural Networks: Pros:
- Can extrapolate well
- Can provide good results. Cons:
- Take longest time to train
- Require extra preprocessing (e.g., normalization)
Resources
-
https://book.fast.ai - The book's website; it's updated regularly with new content and recommendations from everything to GPUs to use, how to run things locally and on the cloud, etc...
-
"Hands-On Gradient Boosting with XGBoost and scikit-learn" - Unread personally, but on my bookshelf and recommended by those in the know.
-
tsai - A time series/sequences focused library built on PyTorch and fastai by Ignacio Oguiza
