A Journey Through Fastbook (AJTFB) - Chapter 8: Collaborative Filtering

fastai

fastbook

collaborative filtering

latent factors

embeddings

recommender systems

recsys

This chapter of “Deep Learning for Coders with fastai & PyTorch” moves us away from computer vision to collaborative filtering (think recommendation systems). We’ll explore building these models using the traditional “dot product” approach and also using a neural network, but we’ll begin by covering the idea of “latent factors,” which are both important for colloborative and tabular models. Lets go!

Author

Wayde Gilliam

Published

March 31, 2022

Collaborative Filtering

What is it?

Think recommender systems which “look at which products the current user has used or liked, find other users who have used or liked similar products, and then recommend other products that those users have used or liked.”

The key to making collaborative filtering and tabular models, is the idea of latent factors.

What are “latent factors” and what is the problem they solve?

Remember that models can only work with numbers, and while something like “price” can be used to accurately reflect the value of a house, how do we represent numerically concepts like the day of week, the make/model of a car, or the job function of an employee?

The answer is with latent factors.

In a nutshell, latent factors are numbers associated to a thing (e.g., day of week, model of car, job function, etc…) that are learnt during model training. At the end this process, we have numbers that provide a representation of the thing we can use and explore in a variety of ways. These factors are called “latent” because we don’t know what they are beforehand.

Note

The learnt numbers for “a thing” may vary to one degree or another based on the data used during training and your objective. For example, what “Sunday” means may be represented differently when you are trying to forecast how many bottle of scotch will be sold that day than if you were trying to predict the number of options that will be traded for a certain equity.

Important

Latent factors allows us to learn a numerical representation of a thing (especially those for which a single number would not do it justice)

If we had something like this …

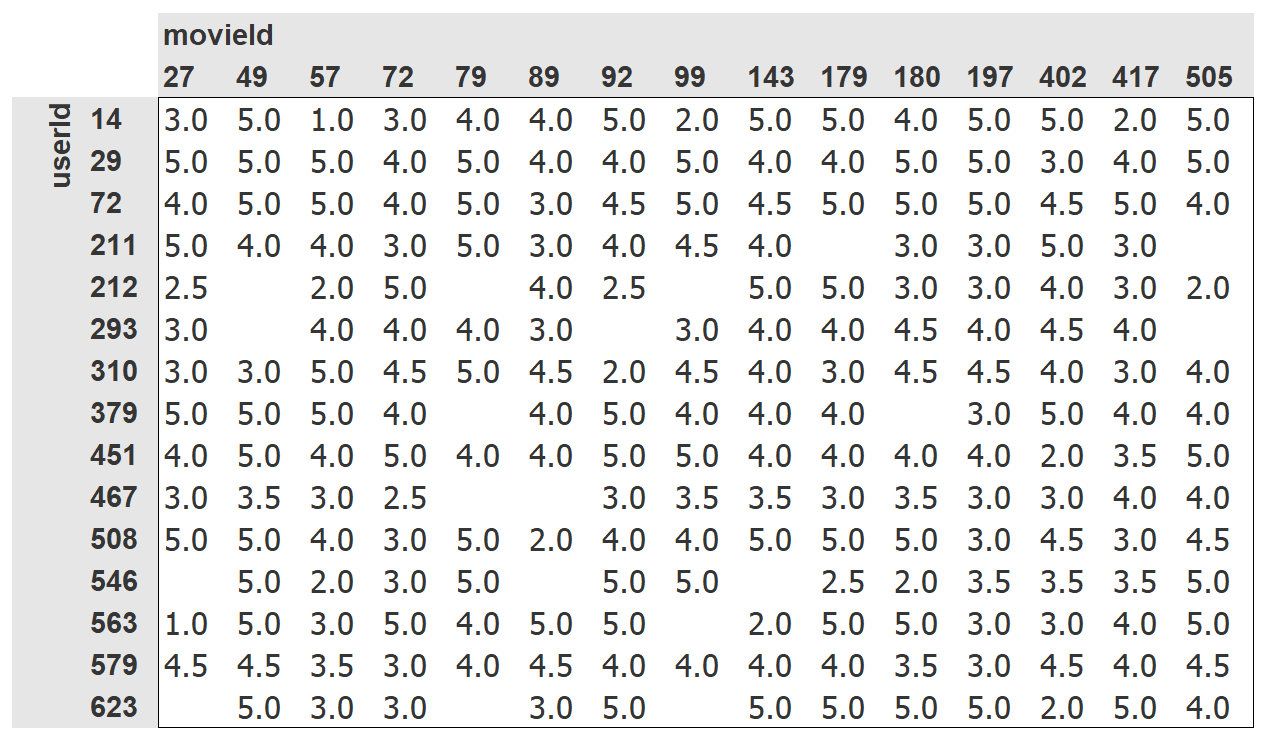
… how could we predict what users would rate movies they have yet to see? Let’s take a look.

from fastai.collab import *
from fastai.tabular.all import *

path = untar_data(URLs.ML_100k)

100.15% [4931584/4924029 00:00<00:00]

ratings_df = pd.read_csv(path/"u.data", delimiter="\t", header=None, names=["user", "movie", "rating", "timestamp"])
ratings_df.head()

	user	movie	rating	timestamp
0	196	242	3	881250949
1	186	302	3	891717742
2	22	377	1	878887116
3	244	51	2	880606923
4	166	346	1	886397596

How do we numerically represent user 196 and movie 242? With latent factors we don’t have to know, we can have such a representation learnt using SGD.

How do we set this up?

“… randomly initialized some parameters [which] will be a set of latent factors for each user and movie.”
“… to calculate our predictions [take] the dot product of each movie with each user.
“… to calculate our loss … let’s pick mean squared error for now, since that is one reasonable way to represent the accuracy of a prediction”

Note

dot product = element-wise multiplication of two vectors summed up.

With this in place, “we can optimize our parameters (the latent factors) using stochastic gradient descent, such as to minimize the loss.” In a picture, it looks like this …

Important

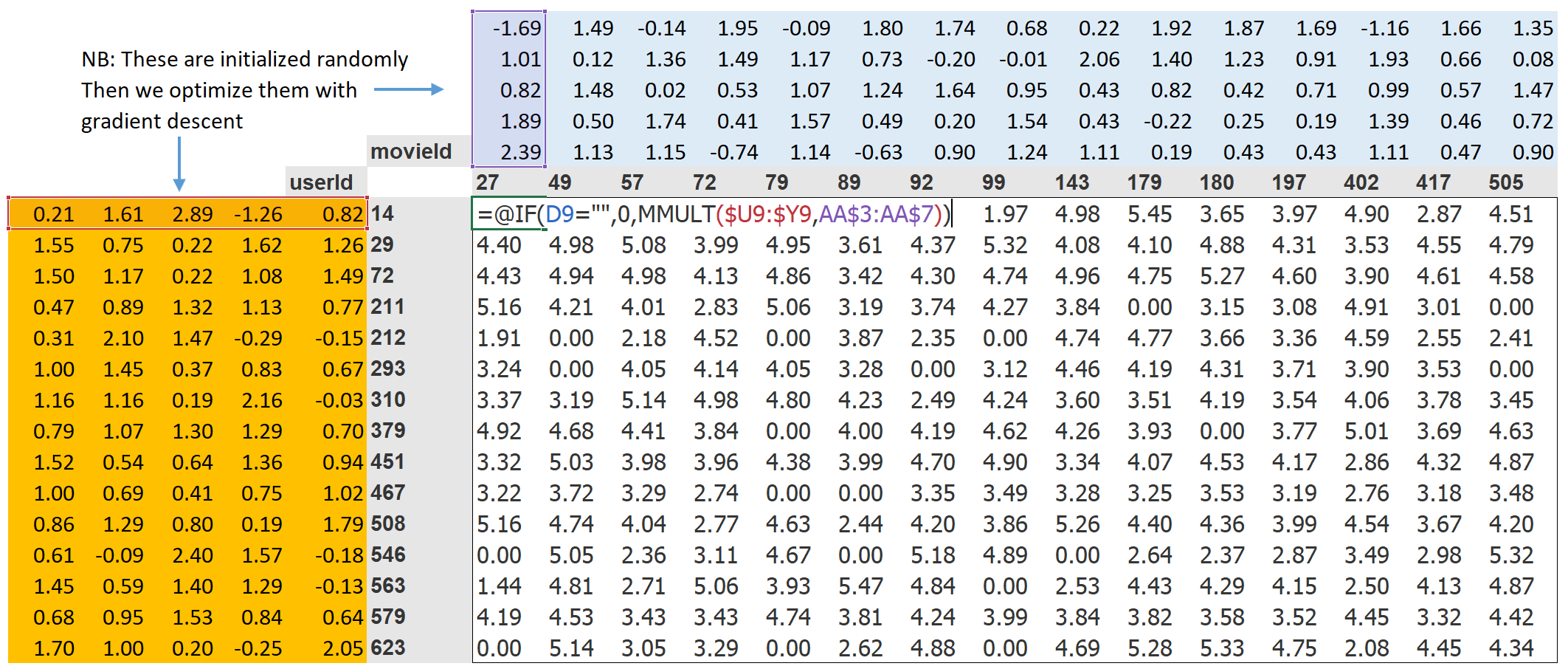
The parameters we want to optimize are the latent factors!

movies_df = pd.read_csv(path/"u.item", delimiter="|", header=None, names=["movie", "title"], usecols=(0,1), encoding="latin-1")
movies_df.head()

	movie	title
0	1	Toy Story (1995)
1	2	GoldenEye (1995)
2	3	Four Rooms (1995)
3	4	Get Shorty (1995)
4	5	Copycat (1995)

ratings_df = ratings_df.merge(movies_df)
ratings_df.head()

	user	movie	rating	timestamp	title
0	196	242	3	881250949	Kolya (1996)
1	63	242	3	875747190	Kolya (1996)
2	226	242	5	883888671	Kolya (1996)
3	154	242	3	879138235	Kolya (1996)
4	306	242	5	876503793	Kolya (1996)

dls = CollabDataLoaders.from_df(ratings_df, item_name="title", user_name="user", rating_name="rating")
dls.show_batch()

	user	title	rating
0	647	Men in Black (1997)	2
1	823	Twelve Monkeys (1995)	5
2	894	Twelve Monkeys (1995)	4
3	278	In & Out (1997)	2
4	234	Pinocchio (1940)	4
5	823	Phenomenon (1996)	4
6	268	Nell (1994)	3
7	293	Mrs. Doubtfire (1993)	3
8	699	Rock, The (1996)	4
9	405	Best of the Best 3: No Turning Back (1995)	1

So how do we create these latent factors for our users and movies?

“We can represent our movie and user latent factor tables as simple matrices” that we can index into. But as looking up in an index is not something our models know how to do, we need to use a special PyTorch layer that will do this for us (and more efficiently than using a one-hot-encoded, OHE, vector to do the same).

And that layer is called an embedding. It “indexes into a vector using an integer, but has its derivative calcuated in such a way that it is identical to what it would have been if it had done a matric multiplication with a one-hot-encoded vector.”

Important

An embedding is the “thing that you multiply the one-hot-encoded matrix by (or, using the computational shortcut, inex into directly)”

Collaborative Filtering: From Scratch (dot product)

A dot product approach

n_users = len(dls.classes["user"])
n_movies = len(dls.classes["title"])
n_factors = 5

print(n_users, n_movies, n_factors)

944 1665 5

class DotProduct(Module):
  def __init__(self, n_users, n_movies, n_factors):
      super().__init__()
      self.users_emb = Embedding(n_users, n_factors)
      self.movies_emb = Embedding(n_movies, n_factors)

  def forward(self, inp):
    users = self.users_emb(inp[:,0])
    movies = self.movies_emb(inp[:,1])
    return (users * movies).sum(dim=1)

model = DotProduct(n_users=n_users, n_movies=n_movies, n_factors=n_factors)
learn = Learner(dls, model, loss_func=MSELossFlat())

learn.fit_one_cycle(5, 5e-3)

epoch	train_loss	valid_loss	time
0	4.443892	3.739447	00:17
1	1.088801	1.125219	00:12
2	0.960021	0.994215	00:09
3	0.917181	0.959309	00:09
4	0.903602	0.957268	00:09

Tip 1: Constrain your range of predictions using `sigmoid_range`

“… to make this model a little bit better … force those predictions to be between 0 and 5. One thing we discovered empirically is that it’s better to have the range go a little bit over 5, so we use (0, 5.5)”

class DotProduct(Module):
  def __init__(self, n_users, n_movies, n_factors, y_range=(0, 5.5)):
      super().__init__()
      self.users_emb = Embedding(n_users, n_factors)
      self.movies_emb = Embedding(n_movies, n_factors)
      self.y_range = y_range

  def forward(self, inp):
    users = self.users_emb(inp[:,0])
    movies = self.movies_emb(inp[:,1])
    return sigmoid_range((users * movies).sum(dim=1), *self.y_range)

model = DotProduct(n_users=n_users, n_movies=n_movies, n_factors=50)
learn = Learner(dls, model, loss_func=MSELossFlat())

learn.fit_one_cycle(5, 5e-3)

epoch	train_loss	valid_loss	time
0	1.012296	0.994128	00:09
1	0.855805	0.903300	00:09
2	0.707656	0.875159	00:09
3	0.482094	0.879115	00:09
4	0.369521	0.884585	00:09

Tip 2: Add a “bias”

Important

A bias allows your model to learn an overall representation of a thing, rather than just a bunch of characteristics.

“One obvious missing piece is that some users are just more positive or negative in their recommendations than others, and some movies are just plain better or worse than others. But in our dot product representation, we do not have any way to encode either of these things … **because at this point we have only weights; we don’t have biases”

class DotProduct(Module):
  def __init__(self, n_users, n_movies, n_factors, y_range=(0, 5.5)):
      super().__init__()
      self.users_emb = Embedding(n_users, n_factors)
      self.users_bias = Embedding(n_users, 1)

      self.movies_emb = Embedding(n_movies, n_factors)
      self.movies_bias = Embedding(n_movies, 1)

      self.y_range = y_range

  def forward(self, inp):
    # embeddings
    users = self.users_emb(inp[:,0])
    movies = self.movies_emb(inp[:,1])

    # calc our dot product and add in biases 
    # (important to include "keepdim=True" => res.shape = (64,1), else will get rid of dims equal to 1 and you just get (64))
    res = (users * movies).sum(dim=1, keepdim=True)
    res += self.users_bias(inp[:,0]) + self.movies_bias(inp[:,1])

    # return our target constrained prediction
    return sigmoid_range(res, *self.y_range)

model = DotProduct(n_users=n_users, n_movies=n_movies, n_factors=50)
learn = Learner(dls, model, loss_func=MSELossFlat())

learn.fit_one_cycle(5, 5e-3)

epoch	train_loss	valid_loss	time
0	0.925160	0.938387	00:10
1	0.807021	0.863466	00:11
2	0.607999	0.871146	00:10
3	0.412089	0.897263	00:10
4	0.294376	0.905192	00:10

Tip 3: Add “weight decay”

Adding in bias has made are model more complex and therefore more prone to overfitting (which seems to be happening here).

Note

Overfitting is where your validation stops improving and actually starts to get worse.

What do you do when your model overfits?

We can solve this via data augmentation or by including one or more forms of regularization (e.g., a means to “encourage the weights to be as small as possible”.

What is “weight decay” (aka “L2 regularization”)?

“… consists of adding to your loss function the sum of all the weights squared.”

Why do that?

“Because when we compute the gradients, it will add a contribution to them that will encourage the weights to be as small as possible.”

Why would this prevent overfitting?

“The idea is that the larger the coefficients are, the sharper canyons we will have in the loss function…. Letting our model learn high parameters might cause it to fit all the data points in the training set with an overcomplex function that has very sharp changes, which will lead to overfitting.

Important

“Limiting our weights from growing too much is going to hinder the training of the model but it will yield a state where it generalizes better”

How do we add weight decay into are training?

“… wd is a parameter that **controls that sum of squares we add to our loss” as such:

model = DotProduct(n_users=n_users, n_movies=n_movies, n_factors=50)
learn = Learner(dls, model, loss_func=MSELossFlat())

learn.fit_one_cycle(5, 5e-3, wd=0.1)

epoch	train_loss	valid_loss	time
0	0.934345	0.946092	00:10
1	0.862484	0.866700	00:10
2	0.715633	0.829172	00:10
3	0.597503	0.817248	00:10
4	0.473108	0.817725	00:10

Creating our own Embedding Module

pp.265-267 show how to write your own nn.Module that does what Embedding does. Here are some of the important bits to pay attention too …

“… optimizers require that they can get all the parameters of a module from the module’s parameters method, so make sure to tell nn.Module that you want to treat a tensor as a parameters using the nn.Parameter class like so:

class T(Module):
  def __init__(self):
    self.a = nn.Parameter(torch.ones(3))

Important

“All PyTorch modules use nn.Parameter for any trainable parameters.

class T(Module):
  def __init__(self):
    self.a = nn.Liner(1, 3, bias=False)

t = T()
t.parameters()   #=> will show all the weights of your nn.Linear
type(t.a.weight) #=> torch.nn.parameter.Parameter

Now, given a method like this …

def create_params(size):
  return nn.Parameter(torch.zeros(*size).normal_(0, 0.01))

… we can create randomly initialized parameters, included parameters for our latent factors and biases like this:

self.users_emb = create_params([n_users, n_factors])
self.users_bias = create_params([n_users])

Interpreting Embeddings and Biases

Note

“… interesting to see what parameters it has discovered … easiest to interpret are the biases”

movie_bias = learn.model.movies_bias.weight.squeeze() # => squeeze will get rid of all the single dimensions
idxs = movie_bias.argsort()[:5]                       # => "argsort()" returns the indices sorted by value
[dls.classes["title"][i] for i in idxs]               # => look up the movie title in dls.classes

['Children of the Corn: The Gathering (1996)',
 'Big Bully (1996)',
 'Showgirls (1995)',
 'Lawnmower Man 2: Beyond Cyberspace (1996)',
 'Free Willy 3: The Rescue (1997)']

“Think about what this means …. It tells us not just whether a movie is of a kind that people tend not to enjoy watching, but that people tend to not like watching it even if it is of a kind that they would otherwise enjoy!”

To get the movies by highest bias:

idxs = movie_bias.argsort(descending=True)[:5]
[dls.classes["title"][i] for i in idxs]

['Titanic (1997)',
 "Schindler's List (1993)",
 'As Good As It Gets (1997)',
 'L.A. Confidential (1997)',
 'Shawshank Redemption, The (1994)']

Note

To visualize embeddings with many factors, you “can pull out the most important underlying directions” using a dimensionality reduction model like principal components analysis (PCA).

See p.268 and these three StatQuest videos for more on how PCA works (btw, StatQuest is one of my top data science references so consider subscribing to his channel). Video 1, Video 2, and Video 3

Collaborative Filtering: Using `fastai.collab`

learn = collab_learner(dls, n_factors=50, y_range=(0, 5.5))
learn.fit_one_cycle(5, 5e-3, wd=0.1)

epoch	train_loss	valid_loss	time
0	0.950606	0.930099	00:10
1	0.834664	0.870282	00:10
2	0.723968	0.833274	00:10
3	0.573679	0.819824	00:10
4	0.489258	0.820394	00:10

learn.model

EmbeddingDotBias(
  (u_weight): Embedding(944, 50)
  (i_weight): Embedding(1665, 50)
  (u_bias): Embedding(944, 1)
  (i_bias): Embedding(1665, 1)
)

movie_bias = learn.model.i_bias.weight.squeeze() 
idxs = movie_bias.argsort()[:5]                   
[dls.classes["title"][i] for i in idxs]

['Children of the Corn: The Gathering (1996)',
 'Showgirls (1995)',
 'Barb Wire (1996)',
 'Island of Dr. Moreau, The (1996)',
 'Cable Guy, The (1996)']

Embedding Distance

“Another thing we can do with these learned embeddings is to look at distance.”

Why do this?

“If there were two movies that were nearly identical, their embedding vectors would also have to be nearly identical …. There is a more general idea here: movie similairty can be defined by the similarity of users who like those movies. And that directly means that the distance between two movies’ embedding vectors can define that similarity”

movie_factors = learn.model.i_weight.weight
idx = dls.classes["title"].o2i["Silence of the Lambs, The (1991)"]
dists = nn.CosineSimilarity(dim=1)(movie_factors, movie_factors[idx][None])
targ_idx = dists.argsort(descending=True)[1]
dls.classes["title"][targ_idx]

'Dial M for Murder (1954)'

Bootstrapping

The bootstrapping problem asks how we can make recommendations when we have a new user for which no data exists or a new product/movie for which no reviews have been made?

The recommended approach “is to use a tabular model based on user metadata to construct your initial embedding vector. When a new user signs up, think about what questions you could ask to help you understand their tastes. Then you can create a model in which the dependent variable is a user’s embedding vector, and the independent variables are the results of the questions that you ask them, along with their signup metadata.”

Important

Be aware of the “problem of representation bias” (e.g., where a few very active users end up skewing the results).

See p.271 for more information on how collaborative models may contribute to positive feedback loops and how humans can mitigate by being part of the process.

Collaborative Filtering: From Scratch (NN)

A neural network approach requires we “take the results of the embedding lookup and concatenate those activations together. This gives us a matrix we can then pass through linear layers and nonlinearities…”

Note

Because “we’ll be concatenating the embedding matrices, rather than taking their dot product, the two embedding matrices can have different sizes (different numbers of latent factors)”

How do we determine the number of latent factors a “thing” should have?

Use get_emb_sz to return “the recommended sizes for embedding matrices for your data, **based on a heuristic that fast.ai has found tends to work well in practice”

embs = get_emb_sz(dls)
embs

[(944, 74), (1665, 102)]

class CollabNN(Module):
  def __init__(self, user_sz, item_sz, y_range=(0, 0.5), n_act=100):
    self.user_factors = Embedding(*user_sz)
    self.item_factors = Embedding(*item_sz)
    self.layers = nn.Sequential(
      nn.Linear(user_sz[1] + item_sz[1], n_act),
      nn.ReLU(),
      nn.Linear(n_act, 1)
    )
    self.y_range = y_range

  def forward(self, x):
    embs = self.user_factors(x[:,0]), self.item_factors(x[:,1])
    x = self.layers(torch.cat(embs, dim=1))
    return sigmoid_range(x, *self.y_range)

model = CollabNN(*embs)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.1)

epoch	train_loss	valid_loss	time
0	10.594646	10.379806	00:11
1	10.368298	10.379800	00:10
2	10.565783	10.379800	00:10
3	10.439667	10.379800	00:10
4	10.356900	10.379800	00:10

If we use the collab_learner, will will calculate our embedding sizes for us and also give us the option of defining how many more layers we want to tack on via the layers parameter. All we have to do is tell it to use_nn=True to use a NN rather than the default dot-product model.

learn = collab_learner(dls, use_nn=True, y_range=(0,0.5), layers=[100,50])

learn.model

EmbeddingNN(
  (embeds): ModuleList(
    (0): Embedding(944, 74)
    (1): Embedding(1665, 102)
  )
  (emb_drop): Dropout(p=0.0, inplace=False)
  (bn_cont): BatchNorm1d(0, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (layers): Sequential(
    (0): LinBnDrop(
      (0): Linear(in_features=176, out_features=100, bias=False)
      (1): ReLU(inplace=True)
      (2): BatchNorm1d(100, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (1): LinBnDrop(
      (0): Linear(in_features=100, out_features=50, bias=False)
      (1): ReLU(inplace=True)
      (2): BatchNorm1d(50, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): LinBnDrop(
      (0): Linear(in_features=50, out_features=1, bias=True)
    )
    (3): SigmoidRange(low=0, high=0.5)
  )
)

learn.fit_one_cycle(5, 5e-3, wd=0.1)

epoch	train_loss	valid_loss	time
0	10.274985	10.379872	00:12
1	10.555515	10.379800	00:12
2	10.436097	10.379800	00:12
3	10.481320	10.379800	00:12
4	10.400410	10.379800	00:12

Why use a neural network (NN)?

Because “we can now directly incorporate other user and movie information, date and time information, or any other information that may be relevant to the recommendation.”

We’ll see this when we look at TabularModel (of which EmbeddingNN is a subclass with no continuous data [n_cont=0] and an out_sz=1.

`kwargs` and `@delegates`

Some helpful notes for both are included on pp.273-274. In short …

**kwargs:

**kwargs as a parameter = “put any additional keyword arguments into a dict called kwargs”
**kwargs passed as an argument = “insert all key/value pairs in the kwargs dict as named arguments here.”

@delegates:

“… fastai resolves [the issue of using **kwargs to avoid having to write out all the arguments of the base class] by providing a special @delegates decorator, which automatically changes the signature of the class or function … to insert all of its keyword arguments into the signature.”

Resources

https://book.fast.ai - The book’s website; it’s updated regularly with new content and recommendations from everything to GPUs to use, how to run things locally and on the cloud, etc…

Collaborative Filtering

What are “latent factors” and what is the problem they solve?

Collaborative Filtering: From Scratch (dot product)

Tip 1: Constrain your range of predictions using sigmoid_range

Tip 2: Add a “bias”

Tip 3: Add “weight decay”

Creating our own Embedding Module

Interpreting Embeddings and Biases

Collaborative Filtering: Using fastai.collab

Embedding Distance

Bootstrapping

Collaborative Filtering: From Scratch (NN)

kwargs and @delegates

Resources

Tip 1: Constrain your range of predictions using `sigmoid_range`

Collaborative Filtering: Using `fastai.collab`

`kwargs` and `@delegates`